When you are drawing a graph of a line segment, then it is necessary to find the midpoint. In math the midpoint is the halfway of a line segment, it can be fun to find the midpoint by the Midpoint calculator. You can say the mid points are the average of the points in cartesian coordinates. You may be considering how to find the midpoint of points (x1, x2), (y1, y2), find the midpoint by adding the points x1 and x2 and then dividing them by 2. The average of the points actually enable us to find the midpoint in 2 dimension and 3 dimensional plan.
What is the midpoint formula?
The midpoint formula is adding the two points x1 and x2 and then dividing them by 2. The same process is done with the y1 and y2 and then divide them by 2. It is actually the average of the points, and we would be able to find the middle of the line segment. It can be tricky to find the middle point when we have the decimal or the fractional points, but when you are using our Midpoint calculator. You are simply able to find the middle of the line segment by the online calculator. So it would become simple, how to find the midpoint of a line segment of two dimensions and three dimensional plan.
In the two dimensional plan, the midpoint formula:
Point (x1,x2) and (y1,y2)
The simple formula for the mid point is:
M = (x₁ + x₂/2, y₁ + y₂/2)
We can write the midpoint formula as
Xm = x₁ + x₂/2
Ym = y₁ + y₂/2
Where;
M indicated as midpoint
Xm = x coordinate of midpoint
Ym = y coordinate of midpoint
In three dimension plan we can find the answer as:
Point (x1,x2) (y1,y2) (z1,z2)
M = (x₁ + x₂/2, y₁ + y₂/2, z₁ + z₂/2)
We can write the midpoint formula as
Xm = x₁ + x₂/2
Ym = y₁ + y₂/2
Zm = z₁ + z₂/2
It can be problematic to find the middle point, when we are dealing with the decimal or the fractional points, but when you are using our Midpoint calculator, the task becomes simple and fast.
Example 1:
Consider a cartesian plane, where (x₁ , x₂) are (6 , 8) and (y₁ , y₂) are ( 10, 12). The midpoint formula calculator is used to find the answer of the midpoint in the mid point.
The points are:
(x₁ , x₂) = (6 , 8)
(y₁ , y₂) = (10 , 12)
Now find the midpoint by the following formula:
M = (x₁ + x₂/2, y₁ + y₂/2)
M = (6 + 8)/2, (10+12)/2
M = (14)/2, (22)/2
M =7, 11
(x , y) = (7 , 11)
How to find midpoint distance?

It can be difficult to find the midpoint distance when we are determining the midpoint of decimal points. The Midpoint calculator is simple and fast and makes the task for the user.
Examples 2:
Consider (x,y,z) plan, here (x₁ , x₂) are (5 , 10) , (y₁ , y₂) are (8, 20) and the (z₁ , z₂) (20 , 25).
Then by answer of question is:
(x₁ , x₂) = (5 , 10)
(y₁ , y₂) = (8, 20)
(z₁ , z₂) = (20 , 25)
Solution:
M = (x₁ + x₂/2, y₁ + y₂/2, z₁ + z₂/2)
M = (5+10)/2, (8+20)/2, (20+25)/2
M = (15)/2, (28)/2, (45)/2
Mid points = ( 7.5 ,14, 22.5 )
Where x= 7.5 , y = 14, z = 22.5
The distance of midpoint:
The distance calculated by the Midpoint calculator by the following formula and the we are adding the three axis in the formula, the
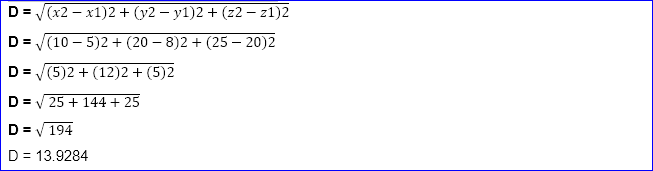
The distance describes the average distance between the points in a three dimensional plan.
Conclusion:
The midpoint is used to draw the graph and the drawing a straight line. It can be tricky to find the midpoint of fractional or decimal points.But you can find the answer in a matter of moments when using the Midpoint calculator. You are even able to find the distance between the points and their exact location in cartesian coordinates and three dimensional plan.You can determine the midpoint of decimal points. The Midpoint calculator is simple and fast and makes the task for the user.It is also a way to learn the midpoints of various geometrical points.







